 Dit artikel verscheen in april 2012 op Gevoelvoorhumus.nl.
Dit artikel verscheen in april 2012 op Gevoelvoorhumus.nl.
Leestijd: ongeveer vier minuten
Voor wie Exponentieel-denkende econoom ontmoet eindig-denkende natuurkundige te lang vond, wil ik hierbij een poging wagen exponentiële groei zo makkelijk uit te leggen, zodat zelfs een politicus het snapt.
Een politicus en een wetenschapper zitten in een afgesloten ruimte. Na een uur merkt de wetenschapper op dat de concentratie van een bepaald schadelijk gas in een uur tijd verdubbeld is van 24 naar 48 ppm (deeltjes per miljoen).
Politicus: "Bij welke concentratie is het dodelijk?"
Wetenschapper: "Bij 25.000 ppm."
Politicus: "Dan hoeven we ons geen zorgen te maken."
Wetenschapper: "Daar ben ik niet zo zeker van."
Politicus: "Onzin. We zitten nog mijlenver van de 25.000 ppm af."
Na twee uur zegt de wetenschapper: "Slecht nieuws. De concentratie is nu 97 ppm. We moeten nu echt op zoek naar het gaslek, want ik denk dat het elk uur verdubbelt. Als dat zo is, dan hebben we nog maar 8 uur de tijd."
Politicus: "Dan hoeven we ons nog steeds geen zorgen te maken. Ik weet zeker dat je ongelijk hebt."
Na drie uur zegt de wetenschapper: "De concentratie is weer verdubbeld naar 195 ppm. We hebben nu nog maar 7 uur de tijd om het lek te vinden."
De politicus zwijgt, maar denkt: wat een zeur.
Na vier uur zegt de wetenschapper: "De concentratie is weer verdubbeld, nu naar 390 ppm. We hebben nog maar 6 uur de tijd om het lek te vinden. Help je nou mee of niet?"
Politicus: "Waarom? We hebben nog bijna 24.000 ppm te gaan. Voor die tijd komt er vast iemand het lek dichten."
Wetenschapper: "Maar het verdubbelt elk uur! We zijn bijna op de helft van de tijd!"
De politicus glimlacht om zoveel simplisme.
Na vijf uur zegt de wetenschapper: "De concentratie is weer verdubbeld naar 781 ppm! We hebben nog maar vijf uur de tijd om het lek te vinden. Als we nu geen actie ondernemen is het misschien te laat!"
Politicus: "Waarom zou ik mijn energie verspillen? Heb nou maar gewoon een beetje vertrouwen. In vijf uur tijd is het van 24 naar 781 ppm gegaan. Dat is nog heel ver van 25.000 vandaan hoor!"
Wetenschapper: "Snap je het echt niet? Wacht, ik zal het uittekenen:"
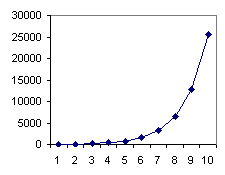
"Zie je hoe verraderlijk dat is? In het begin gaat het langzaam, maar daarna steeds sneller! Halverwege is de concentratie inderdaad nog heel laag, maar neemt daarna in hoog tempo toe!"
Politicus: "Ik vind jou een alarmist. Ik merk nog niet eens dat er gas in de lucht zit en jij roept al dat we doodgaan. Beetje overdreven, niet?"
Wetenschapper: "Daar gaat het niet om, je kan uitrekenen hoeveel tijd er nog is, en dat is niet veel."
Politicus: "Zoek maar hoor, ik zit lekker."
De wetenschapper zoekt, maar kan het in zijn eentje niet vinden.
Na zes uur zegt de wetenschapper: "De concentratie is verdubbeld naar 1562 ppm. We hebben nu nog maar vier uur over. Help alsjeblieft mee!"
Politicus: "Als het boven de 20.000 uitkomt, dan begin ik me pas zorgen te maken. Eerder niet."
De wetenschapper kan uit wanhoop niets meer verzinnen om te zeggen. Hij heeft het toch duidelijk uitgelegd?
Na 7 uur zegt de wetenschapper: "De concentratie is nu al 3125 ppm. Nog maar drie uur over. Help nou toch!"
Politicus: "Nog 16.875 ppm te gaan, jongeman. Dan help ik. Beloofd."
Wetenschapper: "Maar dat is toch veel te laat!"
Politicus: "Geen zorgen, ik weet wat ik doe."
Na acht uur zegt de wetenschapper: "De concentratie is nu al 6250 ppm. We hebben nu echt nog maar twee uur over."
Politicus: "Dacht je dat ik zo ver was gekomen in de politiek als ik niet wist wat ik deed? Just-in-time is altijd het meest economische."
Wetenschapper: "Het gaat niet om economie, maar om onze levens!"
Na negen uur zegt de wetenschapper: "De concentratie is nu al 12.500 ppm. Over ruim een half uur bereikt de concentratie de 20.000 ppm. Maar daarna hebben we echt nog maar 20 minuten over! En ik begin me al licht in het hoofd te voelen."
Politicus: "Over een half uur al? Dat is sneller dan ik had verwacht."
Wetenschapper: "Kijk nog maar eens naar mijn tekening, misschien snap je het nu beter?"
Politicus: "Ja, ik geloof het wel. In het laatste uur gaat de concentratie van 12.500 naar 25.000. Nu snap ik wat je bedoelt met die verdubbelingen. In het begin stelt het niet veel voor, maar naar mate de tijd vordert gaat het steeds sneller. Oké, ik help met zoeken. Ik begin me ook wel een beetje duizelig te voelen."
Wetenschapper: "Eindelijk! Kom op!"
Omdat de politicus erg traag van begrip was liep het bijna mis. Gelukkig kan ik hier een happy end neerschrijven, het is tenslotte maar een voorbeeld. De politicus is echter exemplarisch voor bijna alle politici; rechts en links. Maar of een echte politicus het zou snappen vóórdat het te laat is, dat is vraag.
Helaas is er in de echte wereld een bijkomend probleem: inertie. Allereerst natuurlijk die van de politiek, die rustig blijft zitten terwijl de wetenschapper moord en brand schreeuwt. Maar ik bedoel de vertraagde reactie van de Aarde: zelfs als we op tijd denken te stoppen met broeikasgassen uitstoten, dan gaat klimaatverandering nog tientallen jaren door. Net als de te lange remweg van een auto die de snelheidslimiet overschrijdt.
Een rekenvoorbeeldje
Als een economie, beginnende in 1850, een stabiele groei doormaakt van 2,8% (om precies te zijn 2,8113827% want dan krijg je mooie ronde getallen), dan zal deze na 25 jaar voor het eerst verdubbelen, in 1875. Na 150 jaar, het jaar 2000, is hij 64 keer zo groot.
Hoe lang duurt het voordat hij 128 (2 x 64) keer zo groot is? Weer 150 jaar? Nee dus. Slechts 25!
Na nog eens 150 jaar, het jaar 2150, is hij 64 keer zo groot als in 2000. Dat viel te verwachten, maar hij is 4096 (64x64) keer zo groot als in het beginjaar 1850.
Na nog eens 150 jaar (anno 2300) is hij 262.144 (64x64x64) keer zo groot als in 1850.
Na nog eens 150 jaar (anno 2450) is hij 16.777.219 (64x64x64x64) keer zo groot als in 1850. Tegen die tijd hebben we 393.216 Aardes nodig om deze economie staande te houden als we voor de eerste 150 jaar 1,5 Aardes nemen als ijkpunt.
Ter vergelijking: bij een stabiele groei van 2% over dezelfde 600 jaar zou hij 'maar' 144.578 keer zo groot zijn geworden. Maar dat is nog nog altijd 11.121 Aardes.
Wat in ieder geval belangrijk is om te weten: als je 70 deelt door het groeipercentage, dan krijg je bij benadering de verdubbelingstijd. Dus bijvoorbeeld 70 gedeeld door 2(%) is 35 jaar. Als een economie al 1.000 jaar bestaat, dan zou die in die eerstvolgende 35 jaar evenveel moeten groeien als in de 1.000 jaar ervoor. Dat is eigen aan exponentiële groei.
Politici die eeuwige economische groei aanhangen hebben alle realiteitszin verloren. Geef ze geen stem bij de komende verkiezingen!
Bonus: een animatie! (na 18 minuten gaat het pas over exponentiële groei, maar de rest is ook interessant)
There's No Tomorrow (titel is een doordenkertje, neem hem niet letterlijk)
